Coefficient Of Friction (COF) is a measure of the resistance between two surfaces. It can also be defined as the ratio of friction to a normal reaction. For example,
COF = Friction / Normal Reaction
Here,
- Friction – when we push an object across a floor, it moves slower due to an opposing force called friction.
- Normal Reaction – when two bodies are in contact with each other, they exert a force on one another called a normal reaction.
Properties of the coefficient of friction
- We use the Greek symbol Mu (μ) to represent the COF.
- It is a unitless and dimensionless quantity.
- Its value depends on the material of the objects.
- An object can only slide if the coefficient of friction is greater than 1. Otherwise, it cannot slide.
How to find the coefficient of friction?
Let a body be at rest on a horizontal table as shown in the figure below.
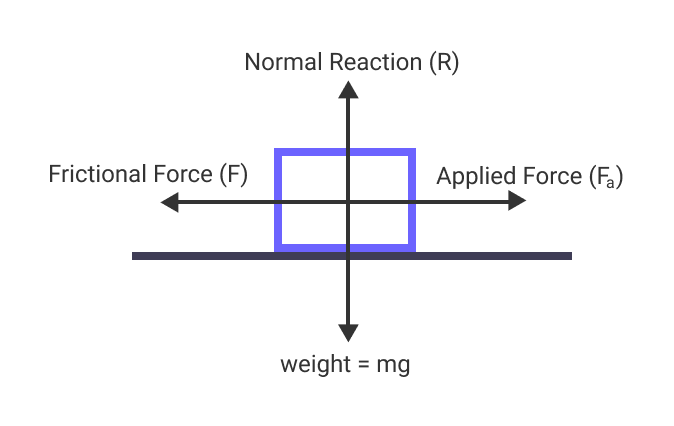
When a force F is applied on it horizontally, the body just begins to slide along the surface. From the laws of friction, the force of friction F is proportional to the normal reaction R.
That is,
Friction (F) ∝ Normal Reaction (R)
or, F ∝ R
or, F = μR
where μ is a constant of proportionality called the coefficient of friction between two surfaces in contact.
Therefore,
μ = F / R
What are the different types of friction coefficient?
Based on the types of frictions, COF can be divided into two types
- Coefficient of Static Friction
- Coefficient of Kinetic Friction
1. Coefficient of Static Friction
We can define the coefficient of static friction as the ratio of limiting friction to normal reaction and its symbol is μs.
Hence, the formula of coefficient of static friction is
μs = Limiting Friction (F) / Normal Reaction (R)
Here, Limiting Friction is the maximum static friction at which one body can move over another body.
2. Coefficient of Kinetic Friction
We can define the coefficient of kinetic friction as the ratio of kinetic friction to normal reaction and its symbol is μk.
Hence, the formula of coefficient of kinetic friction is
μk = Kinetic Friction (Fk) / Normal Reaction (R)
Here, Kinetic Friction is the friction between bodies when a body is moving or rolling over another.
Relation between the coefficient of kinetic and static frictions
Since limiting friction is the maximum friction, it is greater than the kinetic friction. Hence,
Limiting Friction (F) > Kinetic Friction (Fk)
or, (F / R ) > (Fk / R )
or, μs > μkHence, the coefficient of limiting friction is always greater than that of kinetic friction.
1. How to find the coefficient of kinetic friction on an incline?
Suppose we have an inclined plane that makes 60 degrees with the horizontal plane and a box is sliding down with an acceleration of 5.62 m/s2. What is the coefficient of kinetic friction between the box and the inclined surface?
Here,
- Angle of inclination (A) = 60 degrees
- Acceleration of the box (a) = 5.62 m/s2
- Coefficient of friction (μk) = ?
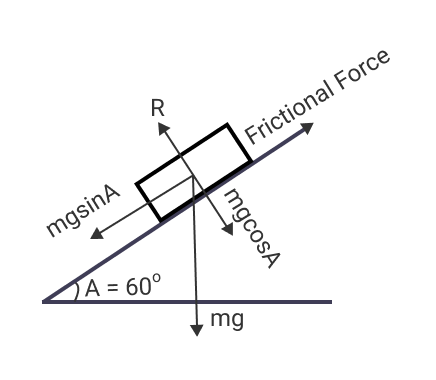
From the above image, the force down the inclined plane is
Force = mgsinA – Frictional Force
We know,
- Force = ma
- Frictional Force = μkR(normal reaction)
Substituting the value
=> ma = mgsinA - μkR
Also, from the image, the value of R is mgCosA. So, our equation becomes
=> ma = mgsinA - μk(mgcosA)
Taking mg common
=> ma = mg (sinA - μkcosA)
removing m from both sides, we get
=> a = g (sinA - μkcosA)
substituting the value of a, g (acceleration due to gravity) and A
=> 5.62 = 9.8 (sin60 - μkcos60)
=> 5.62 / 9.8 = sin60 - μkcos60
we know the value of sin60 is 0.87 and cos60 is 0.5
=> 0.57 = 0.87 - μk0.5
=> μk0.5 = 0.87 - 0.57
=> μk = 0.3 / 0.5
=> μk = 0.6Hence, the coefficient of kinetic friction (sliding friction) is 0.6.
2. What is μk between a block and tabletop?
Suppose a block of mass 6 kg is pushed across the tabletop by a force of 9 Newton. If the block is moving with a constant velocity of 1.8 m/s, find the coefficient of friction between the block and tabletop.
Here,
- Mass of the block (m) = 6 kg
- Force applied (F) = 9 Newton
- Constant speed of block (v) = 1.8 m/s
- μk between block and tabletop = ?
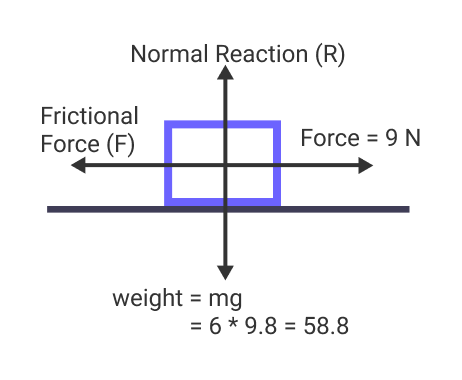
As per our diagram, the force applied on the body is given by
Force Applied = ma + Frictional Force
F = Ff + ma
From our question, we know that the block is moving with constant velocity, hence acceleration (a) becomes 0.
=> F = Ff + m * 0
=> F = FfWe know that the value of frictional force is μkR (reaction force). Substituting the value
=> F = μkR
=> F = μk (mg)
=> μk = F / (mg)
Substituting the value of m, g, and F.
=> μk = 9 / (6 * 9.8)
=> μk = 9 / 58.8
=> μk = 0.15.
Hence, the coefficient of friction between the block and tabletop is 0.15.
Coefficient of Friction of Common Materials
| Materials | Coefficient of static friction | Coefficient of kinetic friction |
|---|---|---|
| Steel on rod | 0.74 | 0.57 |
| Aluminum on steel | 0.61 | 0.47 |
| Copper on steel | 0.53 | 0.36 |
| Brass on steel | 0.51 | 0.44 |
| Copper on cast iron | 1.05 | 0.29 |
| Glass on glass | 0.94 | 0.40 |
| Copper on glass | 0.68 | 0.53 |
| Rubber on concrete (dry) | 1.00 | 0.80 |
| Rubber on concrete (wet) | 0.30 | 0.25 |
Related Article