We can define an escape velocity as the minimum velocity with which a body must be projected vertically upward so that it overcomes the gravitational pull of Earth and never returns.
When we throw an object vertically upwards, it reaches a certain height and comes back to the earth. Now, when we throw it with a greater initial velocity, it reaches greater height before coming back.
In this way, if we keep throwing the object with a certain initial velocity, at some point, the object will go beyond the earth’s gravitational field and escape from the earth.
This minimum initial velocity which can take the object away from earth’s gravitation is known as escape velocity.
What is the formula of the escape velocity?
We can calculate the escape velocity of any object using the following formula.
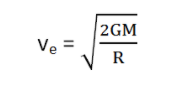
ve = √( 2 G M / R )
where, G is the gravitational universal constant
M is the mass of the Earth from where the object is thrown
R is the radius of Earth
Derivation of Escape Velocity
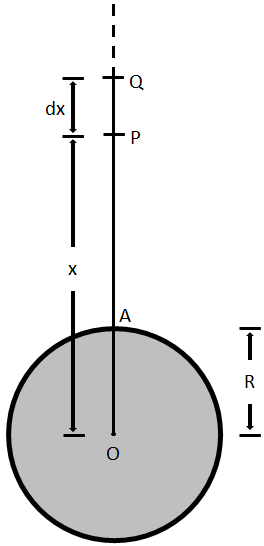
Suppose we have a sphere planet with radius R and mass M. And, a body of mass m is thrown from point A on the earth’s surface.
Let’s join OA and draw it further. Consider two points, P and Q, with distance x and (x + dx) from the center of the Earth O.
Now, suppose the minimum velocity required to escape from the Earth’s surface is ve. Then, the kinetic energy of the object with mass m is
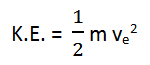
When the object is at point P, (at a distance x from the center of the Earth O), the force of gravity between the object and the Earth is
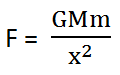
Now, the work done to take the body from P to Q against gravitational force is given by
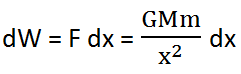
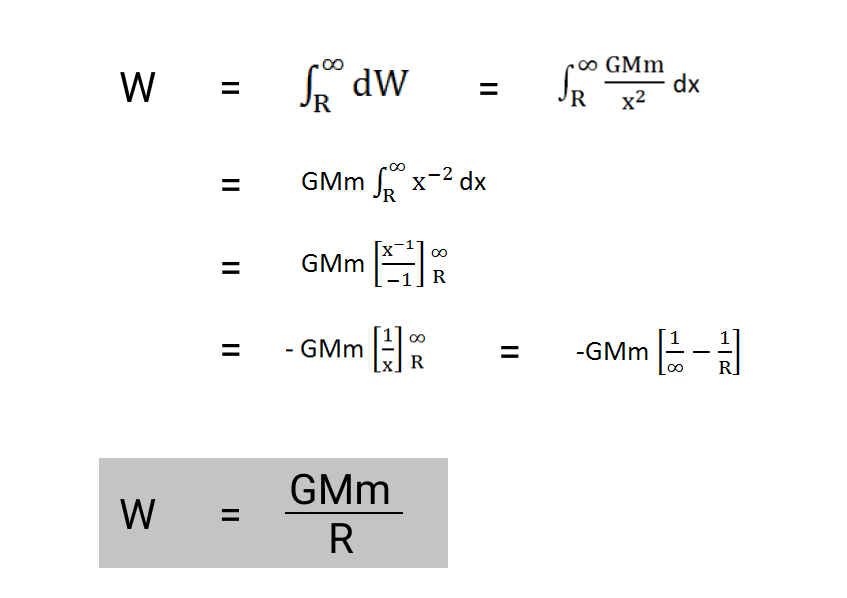
We can calculate the total work done to take the body from the surface of the Earth to infinite against gravitational attraction by integrating the equation within limits: x = R to x = ∞.
Hence, the total work done is
For the object to escape from the Earth’s surface, the kinetic energy given must be equal to the work done against gravity going from the Earth’s surface to infinity.
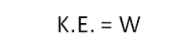
Now, let’s substitute the value of Kinetic Energy and work done against the earth’s gravity.
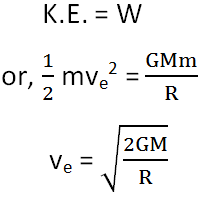
Since we know acceleration due to gravity is given by
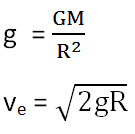
This gives the final formula of the escape velocity.
The relation shows that the escape velocity of an object does not depend on the mass of the projected object but only on the mass and radius of the planet from which it is projected.
What is the escape velocity of the earth?
The escape velocity of the earth is 11.2 km/s which can be calculated using the following formula:
ve = √( 2gR )
In the case of the earth, g (acceleration due to gravity) is 9.8 m/s2, and R (radius) is 6.371 * 106 m. Now, let’s substitute these values in the above equation, we get
ve = √( 2 * 9.8 * 6.371 * 106 )
= √( 11.17 * 106 )
= 11.17 * 103 m/s
ve of Earth is 11.2 km/s
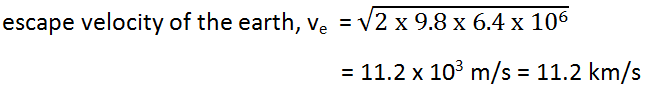
That means a spacecraft leaving the earth’s surface should have 11.2 km/sec or 7 miles/sec initial velocity to escape from the earth’s gravitational field.
Also, due to this high value, gas molecules cannot easily escape from the earth, thus forming the atmosphere around the earth.
Escape Velocity of Sun and Moon
The escape velocity of the sun is very large because of which gas molecules cannot escape the sun. Hence, forming a very firm gaseous envelope around the sun.
On the other hand, the escape velocity of the moon is only 2.4 km/s which is very little. Due to this, gas molecules are also able to escape from the surface of the moon. Hence, there is practically no atmosphere around the moon.