According to law of conservation of energy,
Energy of an isolated system is constant. It can neither be created nor be destroyed but it can be transformed from one type to another.
For example, when an object falls on the ground from a certain height, its kinetic energy is converted into other forms of energy such as sound energy, heat energy, light energy, etc.
Examples of Law of Conversation of Energy
- When petroleum oil is burnt, chemical energy is converted into other form of energy specially light and heat energy.
- In process of generation of hydroelectricity, water in reservoir is flown to rotate the turbine to generate electricity. In this process, potential energy (water in reservoir) is converted to kinetic energy (flowing water) to electrical energy.
- When speaker which doesn’t have battery is turned on, electrical energy is converted to sound energy.
Energy Conservation for a Free Falling Body
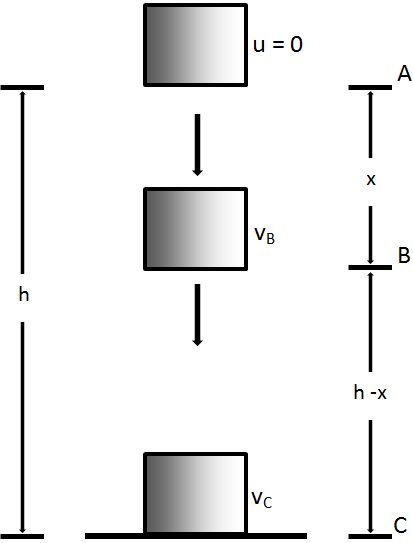
The mechanical energy of a free falling body under the effect of gravity is constant. This is shown in the given figure.
Let us take an object of mass m at a point A, above the ground at a height of h from the ground.
At A, the body is at rest. Thus,
K.E. of the body = 0
P.E. of the body = m g h
Total energy of the body at
A = K.E. + P.E. = 0 + m g h = m g h
Suppose, the body falls freely from A to the ground and at a point B on its path, its height above the ground will become (h – x).
Therefore, potential energy of the body = m g (h – x)
If vB is the velocity at B, then
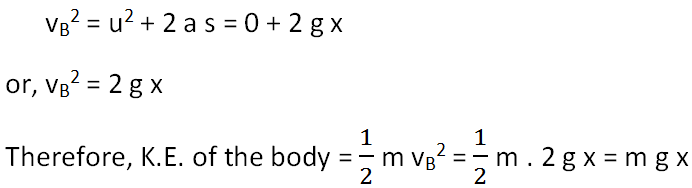
Total energy of the body at
B = K.E. + P.E. = m g (h - x) + m g x = m g h
At point C,
If vC be the velocity of the body at point C (just before striking the ground), then
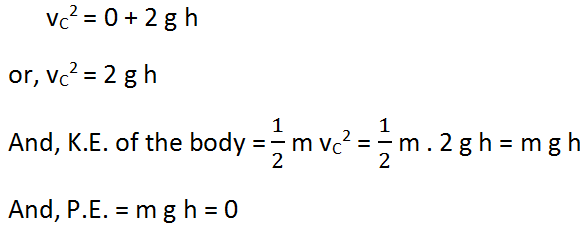
Therefore, total energy at point C = K.E. + P.E. = m g h + 0 = m g h
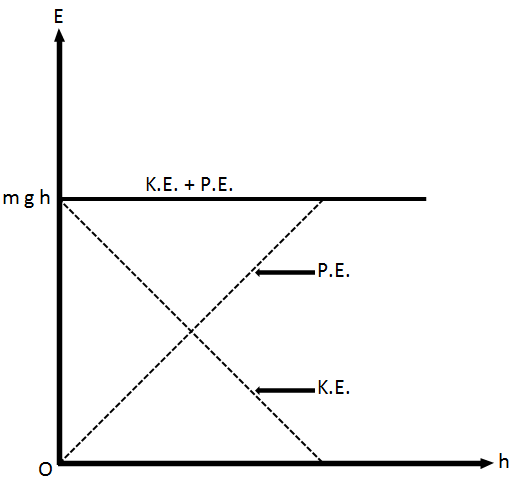
Fig. Variation of kinetic energy and potential energy at different points on the path
Thus, the total mechanical energy of the body remains the same at all points during the downward journey. As the body falls from height h, its potential energy decreases while the kinetic energy begins to increase; the total mechanical energy at any point being the same i.e. m g h. When the body reaches the ground, P.E. = 0 and K.E. is equal to the initial potential energy m g h at the height h. The figure below shows the variation of P.E. and K.E. with height. Similar case can be applied when a body is thrown vertically upward.