Linear Momentum (LM) is the quantity of motion contained in a moving body. It depends upon the mass and velocity of the body. For example,
When a football moving with a 6 km/hr velocity hits us, we won’t feel much. However, if a train moving with a 6 km/hr velocity hits us, we will feel a lot of impacts.
This is because of the linear momentum, which depends on both the mass and velocity of an object.
Formula of Linear Momentum
The product of mass and velocity is the measure of the momentum so, the formula is
P = m * v
where m = the mass of the object
v = velocity of the object moving in a direction
Here, P is the symbol used to represent the linear momentum.
Principle of Conservation of Linear Momentum
The principle of conservation of momentum states that,
If no outer force is applied to the system, the vector sum of the two colliding objects remains constant and is not affected by their collision.
That is, the total momentum before the collision is equal to the total momentum after the collision.
Let us consider an isolated system of n particles having initial momentum p1, p2 … pn. Due to the collision, let the momentum of the particles after collision be p1‘, p2‘ … pn‘, respectively.
Then according to the principle of conservation of linear momentum, in the absence of external force,
p1 + p2 + … + pn = p1' + p2' + … + pn'
Proof of law of conservation of momentum
To prove this principle, let us consider two colliding objects, X and Y, of masses m1 and m2, respectively.
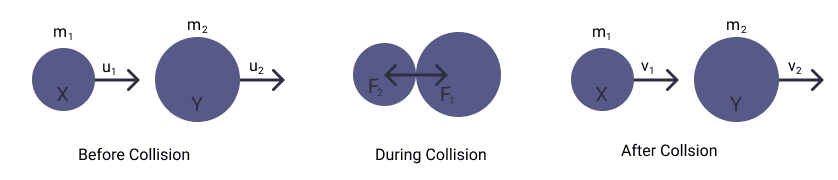
Suppose both objects move on the same straight line before the collision, as shown in the figure. And, the velocities of X and Y are u1 and u2, respectively, such that u1 > u2.
After the collision, let their velocities change to v1 and v2 on the same line.
The collision occurs for a short time interval t, and during the collision, each object will exert a force on the other object.
The force experienced by A is given as
F2 = change in momentum / time
= ( m1v1 - m2u2 ) / t
Similarly, the force experienced by B is
F1 = change in momentum / time
= ( m2v2 - m1u1 ) / t
According to Newton’s third law of motion, the force experienced by A and B is equal and opposite.
F1 = F2 substituting values of F1 and F2
( m2v2 - m1u1 ) / t = ( m1v1 - m2u2 ) / t
( m2v2 - m1u1 ) = ( m1v1 - m2u2 )
This means the total momentum before the collision is equal to the total momentum after the collision if no external force acts on them. Hence, it proves the principle of conservation of linear momentum.
Example: Principle of Conservation of Momentum
Calculate the recoil velocity of a pistol of mass 4.0 kg, which shoots a 0.040 kg bullet at a speed of 280 m s-1. (Assume that the total momentum of the system was 0 before the bullet was fired).
For Bullet
Momentum of Bullet = mass of bullet * velocity of bullet
= 0.040 * 280
= 11.2 kg m s-1For Pistol
Momentum of Pistol = mass of pistol * velocity of pistol
= 4.0 * velocity of pistol
According to the principle of linear momentum, the momentum of the pistol and bullet should be equal and opposite.
Momentum of Pistol = - Momentum of Bullet
substituting the value of momentum of both pistol and bullet
4.0 * velocity of pistol = - 11.2
or, velocity of pistol = 11.2 / 4.0
or, velocity of pistol = - 2.8 ms-1The negative sign indicates that the direction of the pistol is opposite to the direction of the bullet.
Frequently Asked Questions
1. Is linear momentum a vector quantity?
The formula of momentum is
P = mass * velocity
Here, mass is a scalar quantity, and velocity is a vector quantity.
Hence, the linear momentum (P) of a body is also a vector quantity, and it has the same direction as that of velocity.
2. What is the SI unit of linear momentum?
Momentum is the product of mass and velocity. We know that the units of mass and velocity are kg and m/s, respectively.
Hence, the SI unit of momentum is kg m/s.
3. What is the dimensional formula of linear momentum?
The dimensional formula of linear momentum is [M1 L1 T-1]. Let’s derive this using the formula.
P = mass * velocity
We know velocity is given by distance / time.
P = mass * (distance / time)
= mass * distance * time-1
We use the fundamental quantities [M] for mass, [L] for distance, and [T] for time. Hence,
Dimensional Formula of Linear Momentum = [ M1 L1 T-1 ]