Newton’s First Law of Motion
According to Netwon’s first law of motion,
An object in rest continues to be in rest and an object in motion continues to be in motion in a straight line unless external force is applied on it.
From the above statement, we conclude that, to change the state of rest or motion, an external agent is required which is called the force. Internal force does not produce motion in total. The first law gives the definition of force.
First law is also called the Law of Inertia. This mean, a body cannot change its state of rest or motion by its own will. This inability to change the state of a body is called inertia. There are two types of inertia:
- Inertia of rest
- Inertia of motion.
Inertia of rest
The opposition of a body to change its state of rest is called inertia of rest. Examples:
- When a bus suddenly moves, the passenger falls backwards. It is because the lower part of the body of the passenger in contact to the bus is in motion but upper part tends to be at rest. So, the passenger tends to fall backwards.
- When we shake a mango tree, the mangoes fall down. It is because when we shake the tree, the mangoes tend to be at rest due to inertia whereas the branches are in motion. That is why the mangoes get detached from the branches.
- If we suddenly pull a paper over which a stone is kept, the stone remains at rest. It is because the stone tries to remain at rest.
- When we hit a carpet with a stick, the dust particles come out of it. By hitting the carpet, it is set in motion whereas the dust particles remain at rest.
Inertia of motion
The opposition of a body to change its state of motion is called the inertia of motion. Examples:
- When we jump from a moving bus, we fall forward. It is because the foot comes to rest but out upper part is still in motion due to inertia and we fall forward.
- When brakes of a bus are suddenly applied, we tend to fall forward. It is because the lower part in contact to the bus comes at rest whereas the upper part is still in motion. So we fall forward.
Newton’s Second Law of Motion
Newton’s second law of motion state that,
The rate of change of momentum of a body with respect to time is directly proportional to the net external force applied on it and the change takes place in the direction of the force.
When a force F is applied to a body whose momentum at time t is p, then from Newton’s second law:
We have,
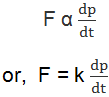
where k is a constant of proportionality, whose value depends upon the choice of unit of force. The system of units are so chosen that k=1.
Therefore,
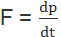

Fig: The momentum of a body changes from P1 to P2 as force F acts on it.
If m is the mass and v is the velocity of the moving object, the linear momentum, p = mv and
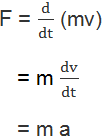
as m is constant for a given body.
Therefore, F = m a
Above equation gives the magnitude of force if we know the mass and the acceleration of the object. As the force causes the change in momentum,, i.e. change in velocity (mass remains constant), Newton’s second law provides a way to compute the Force.
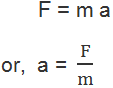
That is, more is the mass for same force, less is the acceleration, i.e, mass opposes the change in the state of motion. So, Newton’s second law of motion tells us that mass is a measure of its inertia.
Newton’s Third Law of Motion
Newton’s Third Law of Motion states that,
For every action there is always an equal and opposite reaction.
According to above statement, forces occur in a pair only because of action and reaction, i.e. isolated force does not exist in nature. Sometime, we may misinterpret the law and think that if there are action and reaction acting on a body, the body must be at rest. But the action and reaction do not act on the same body but act on two different bodies. Due to this reason, action and reaction do not cancel each other.
Let us illustrate the Newton’s third law of motion.
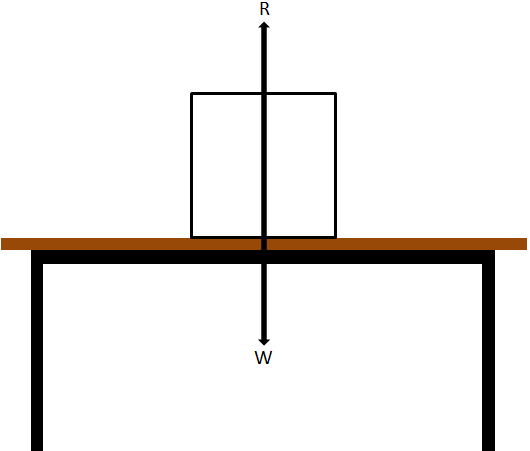
- A block resting on a table. Due to the weight W of the block, it presses on the table by its weight which is taken as action. The table also exerts force on the block equal in magnitude but opposite in direction to that of the weight of the block and called the reaction R. So, the action and reaction acts on two different bodies and W = –R.

- Pushing a block. A man is pushing a block on a smooth horizontal surface with negligible friction. The man exerts a force F1 on the block and the block also exerts a force F2 on the man. To move the block forward, the man must push backward against the ground and the man gets the reaction force which is applied on the block. So the motion of the block is possible.
- Swimming. While swimming in the pond, the swimmer pushes the water in backwards direction whereas the reaction of the water pushes the swimmer in the forward direction. So the swimmer can swim easily in the water.
- Walking. When we are walking on the road, we push the ground in the backwards direction, the man gets reaction force in forward direction.