Newton’s Formula of Velocity of Sound in Gas (Laplace Correction)

Newton’s formula to calculate the velocity of sound in air is,

v = √(P / ρ )

Here, 

  • P = Pressure 
  • ρ = Density of air
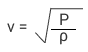
Newton's Formula of velocity of sound in gas

According to Newton, when sound waves travel in the air, compression and rarefaction are formed. He also assumed that the process was very slow, and there was heat exchange during the process.

During the compression, the heat produced is given to the surroundings and the heat loss is gained from the surrounding. Hence, the temperature remains constant and sound waves propagate through an isothermal process.

Derivation: Newton’s Formula of Velocity of Sound in Air

According to Boyle’s law (law of gas), the pressure of the gas is inversely proportional to the volume.


  P ∝ 1 / V

where,

  • P = Pressure
  • V = Volume of air

Hence,


  P = constant / V

  or, PV = constant

Now, let’s differentiate the above equation,


      PdV + VdP = 0

  or, PdV = -VdP

  or, P = - (VdP / dV)

  or, P = dP / - (dV / V)

  or, P = B

where B is the bulk modulus of the air.

If we have B as the bulk modulus and ρ as the density of the air, then the velocity is given by


  v = √(B / ρ )

From the earlier equation, we know that B = P. So, we get the velocity of sound in air as


  v= √(P / ρ )
Derivation of newton's formula of velocity of sound in gas

Calculation: Velocity of Sound using Newton’s Formula

At NTP (Normal Temperature and Pressure), we have

Pressure (P) = 1.1013 * 105 N/m2

Density of air(ρ) = 1.293 kg/m3

Now, we can calculate the velocity as


  v    = √(P / ρ )

       = √(1.1013 * 105 / 1.293 )

  v    = 280 m / s

Flaws in Newton’s Formula

From the above calculation, we have calculated the velocity of sound as 280 m/s. However, experimentally it has been found that the velocity of sound in air is 332 m/s.

This concludes that there is some error in Netwon’s assumption and needs correction.

Laplace Correction of Newton’s Formula

Laplace Correction solves the error in Newton’s formula by providing an assumption.

According to Laplace, compression and rarefaction occur very fast and there is no heat exchange during the compression. Thus, the temperature doesn’t remain constant and the propagation of sound in the gas is an adiabatic process.

Derivation of Laplace Correction

In an Adiabatic Process,


  PVγ = constant

Here, 

  • P = Pressure
  • V = Volume
  • γ = Adiabatic index = Cp / CV
  • Cp = Specific heat for constant pressure
  • CV = Specific heat for constant volume

Differentiating the above equation, we get


  VγdP + PγVγ - 1dV = 0

Dividing both sides by Vγ – 1


      VdP + γPdV = 0

  or, γPdV = - VdP

  or, γP = - VdP / dV

  or, γP = - dP / (dV / V)

  or, γP = B

where B is the bulk modulus of the air.

If we have B as the bulk modulus of the air, γ as the adiabatic index, and ρ as the density, then the velocity of sound is given as


  v = √(B / ρ )

From the earlier equation, we know B = γP. Hence, Laplace Correction gives the velocity of sound in air as


  v = √(γP / ρ )
Derivation of laplace correction for newton's formula to compute velocity of sound in gas

Calculation: Velocity of Sound using Laplace Correction

At NTP (Normal Temperature and Pressure), we have 

Pressure (P) = 1.1013 * 105 N/m2

Density of air (ρ) = 1.293 kg/m3

Adiabatic index (γ) = 1.4

Now, we can calculate the velocity as


  v    = √(γP / ρ )

       = √ ( (1.4 * 1.1013 * 105) / 1.293)

  v    = 332 m/s2

This value is very close to the experimental value. Hence, Laplace Correction provides the correction to Newton’s Formula to compute the velocity of sound in air.