Kinetic Energy
The energy possessed by a body due to its motion is called kinetic energy. So from the definition, it is known that kinetic energy increases with increase in speed of the particle. Few examples of bodies possessing kinetic energy are a moving bus, moving water in a river, a moving bullet, etc.
Expression for Kinetic Energy
Let us consider a block of mass m lying on a smooth horizontal surface as shown in the figure. Let a constant force F be applied on it such that, after traveling a distance s, its velocity becomes v.
If a is the acceleration of the body, then
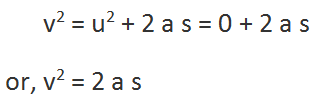
as initial velocity, u = 0. So
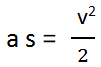
As work done on the body = force X distance, then
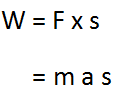
From the equations above, we have
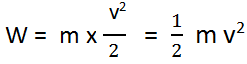
This work done on the body of mass m will set the body moving with velocity v from its state of rest. It is equal to kinetic energy of the body. Therefore,
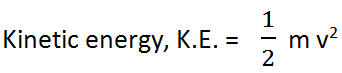
Work-Energy Theorem Statement
The total work done by force acting on a body is the total change in its kinetic energy.
Proof: Work-Energy Theorem
Suppose a body is moving on a smooth horizontal surface with a constant velocity, u. Let a constant force F acts in the body from point A to B as shown in the figure below, such that the velocity increases to v. The work done by the force is,
W = F s
where s is the displacement of the body.
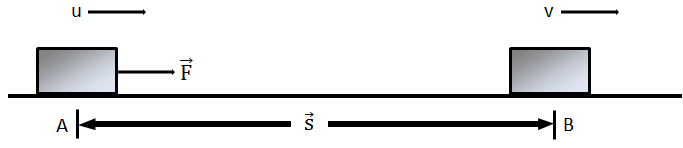
Fig. Work done by the force F over the displacement s of the object is F s.
From Newton’s second law of motion,
F = m a
where m is the mass of the body. Then
W = m a s
From the equation of motion,
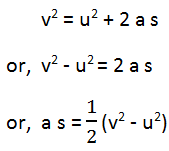
Then,
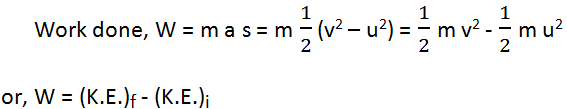
So, the work done on moving the body by the force is equal to the increase in its kinetic energy. Again we can write the above equation as,
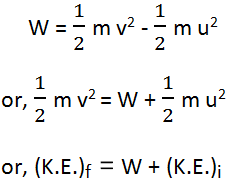
That is, the final kinetic energy of the body is increased and it is the sum of the work done on the body by the applied force and its initial kinetic energy. This principle is called work-energy theorem. If the force acts in the opposite direction to the direction of the motion of the body, the force does the negative work and it is given as,
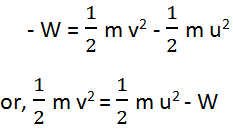
So, the final kinetic energy decreases.