Angular momentum (AM) is a physical quantity possessed by a body moving around a point. Suppose we have an object of mass m, moving with velocity v along a circular path of radius r, then the AM of the object is m * v * r.
We know that mass * velocity gives the linear momentum of the object; hence AM is linear momentum multiplied by the radius of the circular path.
The formula of angular momentum is
L = m * v * r
where m = mass of the object
v = velocity of the object moving in a direction
r = radius of the circle along which the object is moving
Here, L is the symbol used to represent the angular momentum.
Some of the examples are:
- Earth moving around the sun
- The motion of the bicycle wheel
- Electrons revolving around the nucleus
Equation for Angular Momentum
We can also define AM as the product of the linear momentum of the object and the perpendicular distance between the object and the axis of rotation.
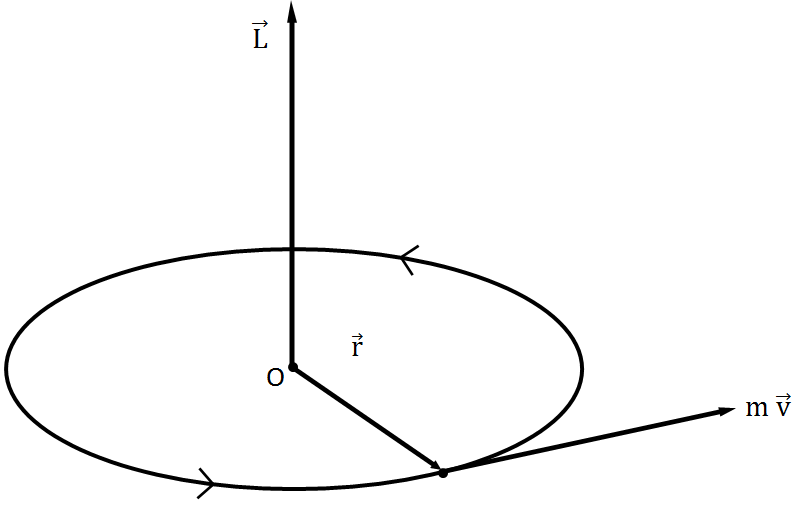
In the above image, we have an object of mass m revolving around the circle of radius r with speed v about an axis passing through center O.
Here, the linear momentum of the object is
P = m v
As we know the AM is the product of linear momentum and perpendicular distance from the axis of rotation so,
L = pr
After replacing the value of P with mv, the equation becomes
L = m v r
Since v = w r, where w is the angular velocity of the object, we can write the equation as
L = m (w r) r
= m r2 w
Also, m r2 is the formula of the moment of inertia (I), so we can write the equation of angular momentum as
L = I w
Principle of Conservation of Angular Momentum
The principle of conservation of angular momentum states that,
“If no external torque acts on a system, the total angular momentum of the system remains constant.”
If I be the moment of inertia of a body about a given axis of rotation and w be its angular velocity, then I w = constant.
This equation represents the mathematical form of the principle of conservation of AM.
Proof
We know that the torque acting on a system is equal to the time rate of change of L of the system about that axis, i.e.
torque (T) = change in angular momentum (dL) / change in time (dt)
If no external torque acts on the system, T = 0. So,
dL / dT = 0
If we perform the mathematical integration on this equation, we get
L = constant
or,
I w = constant
This proves the principle of conservation of angular momentum.
Note:
In general, we also write: I1 w1 = I2 w2
Unit of Angular Momentum
The SI unit of angular momentum is kg m2 s-1, where kg is the kilogram, m is meter, and s is second.
And, in the CGS system, its unit is g cm2 s-1, where g is the gram, cm in centimeter, and s is second.
We can also represent the unit of momentum in terms of Joules.
Unit of Joules = kg m2 s-2
Unit of Angular Momentum (L) = kg m2 s-1We can write s-1 * s in place of s-1.
L = kg m2 s-2 s
Replacing kg m2 s-2 with J (joules).
Unit of Angular momentum in terms of Joules = J s
Dimensional Formula of Angular Momentum
The dimensional formula of angular momentum is [M L2 T-1]. Let’s derive this using the formula.
L = mass * velocity * radius
We know velocity is given by distance / time.
L = mass * (distance / time) * radius
= mass * distance * radius * time-1
We use the fundamental quantities [M] for mass, [L] for both distance and radius, and [T] for time. Hence,
Dimensional Formula of Angular Momentum = [ M L2 T-1 ]
Frequently Asked Questions
1. Is angular momentum a vector quantity?
Angular momentum is a vector quantity because it has both
- magnitude – given by linear momentum multiplied by the radius of the circle
- directions – towards perpendicular to the plane of rotation.
3. How to calculate angular momentum?
If an object has a mass and is moving with a certain velocity along a circular path, then its angular velocity can be calculated using the formula
L = mass * velocity * radius
Let’s see an example. Here, we will calculate the L of the earth moving around the sun.
Mass of earth (m) = 6.0 * 1024 kg
Radius of earth orbit (r) = 6.4 * 106 m
For a rigid body like earth,
Moment of inertia (I) = 0.4 * m * r2
= 0.4 * 6.0 * 1024 * (6.4 * 106)2
= 2.4 * 1024 * 40.96 * 1012
98.304 * 1036The angular velocity (w) of the earth is given by
w = 2 π / T
Here, T is the time taken by earth to complete a rotation (24 hours = 86400 seconds).
w = (2 * 3.14) / 86400
= 7.3 * 10-5Finally,
L for earth = I * w
= (98.304 * 1036) * (7.3 * 10-5)
= 7.1 * 1033Angular Momentum of Earth = 7.1 * 1033
4. What is the conservation of angular momentum?
The conservation of angular momentum states that,
“Angular momentum is always conserved in the world; it can neither be created nor be destroyed, but can be transferred from one body to another”.