In this article, we will learn the center of gravity and its equation. We will also learn about the center of gravity of different shapes.
The center of gravity of a body is a point where the weight of the body acts and the total gravitational torque on the body is zero.
Note:
Don’t get confused between the center of gravity and the center of mass.
Equation of Center of Gravity
To determine the center of gravity (CG) of an irregularly shaped body (say cardboard), we take a narrow tipped object (say a sharp pencil).
Now by trial and error, we can locate a point CG on the cardboard, where it is balanced on the tip of the pencil. This point of balance is the center of gravity of the cardboard.
The tip of the pencil at CG provides the normal reaction R to the total weight mg of the cardboard. The cardboard is in translational equilibrium, as R = mg.
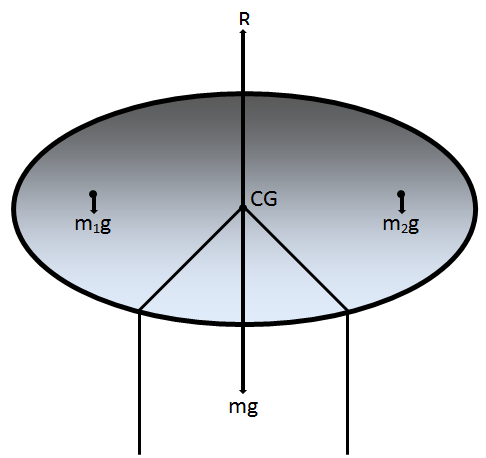
Also, the cardboard is in rotational equilibrium because if it were not so, the cardboard would tilt and fall due to an unbalanced torque.
Force of gravity like m1g, m2g, m3g… etc. acts on individual particles of the cardboard. They make up the torque on the cardboard.
For its particle of mass mi, the force of gravity is mig. If ri is the position vector of this particle from CG of the cardboard, the torque about the CG is
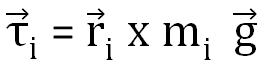
CG of the cardboard is located so that the total torque on it to forces of gravity on all the particles is zero. Thus, total torque is:
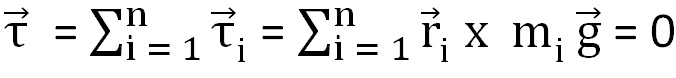
As g is a non-zero value and the same for all particles of the body, so the above equation can be written as
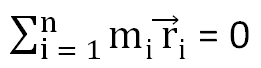
This is the condition when the center of mass of the body lies at the origin. As position vectors are taken with respect to the CG, the center of gravity of the body coincides with the center of mass of the body.
However, if the body is so extended that g varies from part to part of the body, then the center of gravity will not coincide with the center of mass of the body.
For a body of small size, having uniform density throughout, the CG of the body coincides with the center of mass.
In the case of a solid sphere, both CG and the center of mass lie at the center of the sphere.
For a body of very large dimensions and having non-uniform density, the center of gravity does not coincide with the center of mass.
Calculation of Center of Gravity
Calculate the center of gravity of the following diagram:
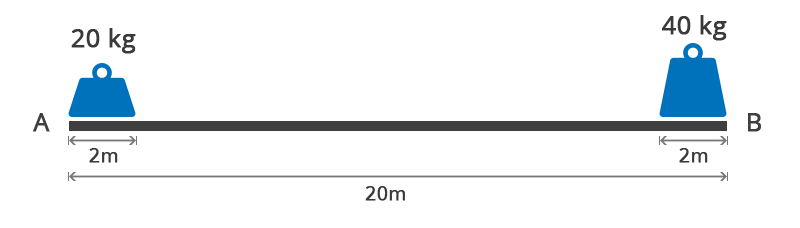
Step 1: Draw Free Body Diagram of the System
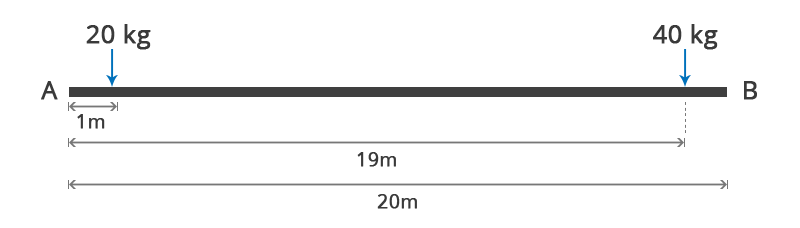
Step 2: Find Weight Distance Moment with Reference to Datum
Datum is the arbitrary starting point on the end of the slab.
Let’s suppose, we choose point A as a datum and find momentum with respect to that point. The total weight distance moment at point A is given by:

Step 3: Calculation of Center of Gravity
To calculate the center of gravity, divide the total weight distance moment by the total mass of the system.

Thus, the center of gravity is 13 meters from the left-hand side.
Shape of a Body and its CG Position
- The center of gravity of a body depends on its shape and size of the body. For example, in a sphere, CG is at the center.
- The CG of a body may not necessarily be within the body. For example, the CG of a ring does not lie in the material of the ring; it is at its geometric center.
- Similarly, in a hollow sphere, the CG is not within the material but lies at its geometric center.
- The position of the center of gravity changes with the change in the shape of a body. For example, an iron bar has CG at its middle point. But when the bar is bent into a circular ring, the CG is not within the material, it is at its geometric center.
- When any rigid body is supported at its CG, it is in equilibrium.
CG of Different Shape of Bodies
| Shape of Body | Position of CG |
|---|---|
| Thin Uniform Bar | middle point of the bar |
| Circular Ring | center of the ring |
| Circular Disk | center of the disk |
| Sphere, Hollow Sphere, Annular Disk | at its center |
| Cubical or Rectangular Block | point of intersection of the diagonals |
| Triangular Lamina | point of intersection of the medians |
| Square Lamina, Paralellogram and Rectangular Lamina | point of intersection of the diagonals |
| Cylinder | middle point of the axis |
| Cone or Pyramid | on the line joining the apex of the center of the base at a distance equal to 1/4 of the length of this line from the base |