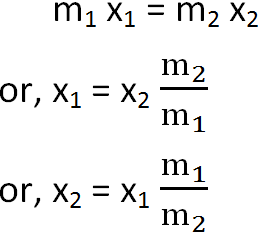The center of mass (not to be confused with center to gravity) of a body is the point which behaves as if all the mass of the body is concentrated there. Thus, if a force acts at this point, the body will accelerate but will not rotate.
A rigid body consists of a large number of particles and the mass of the body is the sum of the masses of individual particles. But, we can consider a point on the body such that the whole mass of the body is concentrated at it and the motion of that point is same as the motion of particles of same mass as that of the body when same force is applied on it. This point is called the center of mass. Thus, center of mass of an object is the point at which an applied force produces linear acceleration but no rotation.
Calculation of Center of Mass
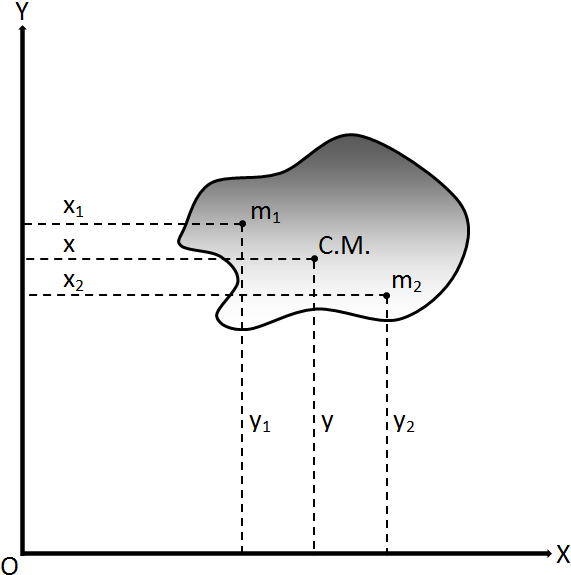
Let us consider a system of n particles of masses m1, m2, m3, … mn with co-ordinate positions (x1,y1), (x2,y2), (x3,y3), … (xn,yn) respectively as shown in the figure. Let (x,y) be the co-ordinate of center of mass of the body. For the various particles, we have F1= m1 a1, F2= m2 a2, F3= m3 a3and so on.
Here F1 is the net external force acting on mass m1 and it produces an acceleration a1. Similarly, F2, F3, … also produce acceleration a2, a3, … respectively. Total force acting on the body,
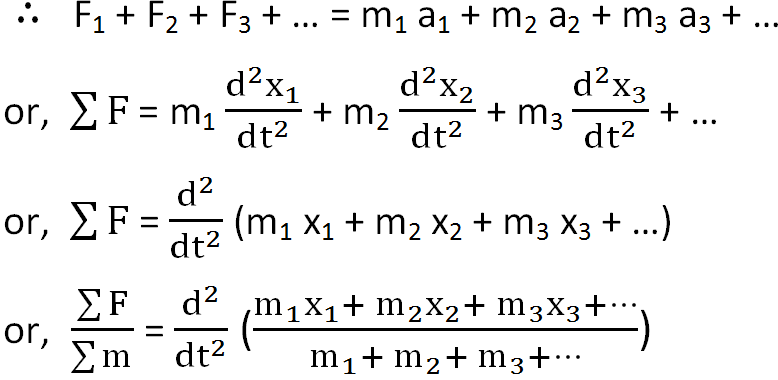
From this relation, we can say that x-coordinate of center of mass is
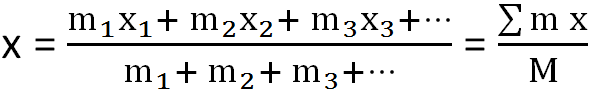
Similarly, its y-coordinate is
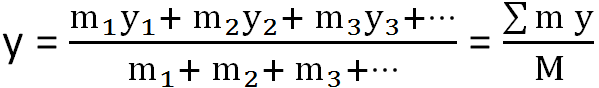
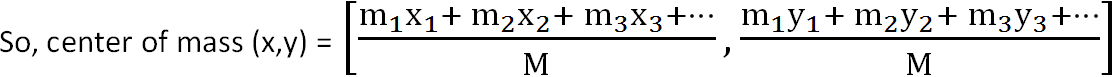
Where M = m1 + m2 + m3 + …, total mass of the body
Center of Mass of Two Bodies
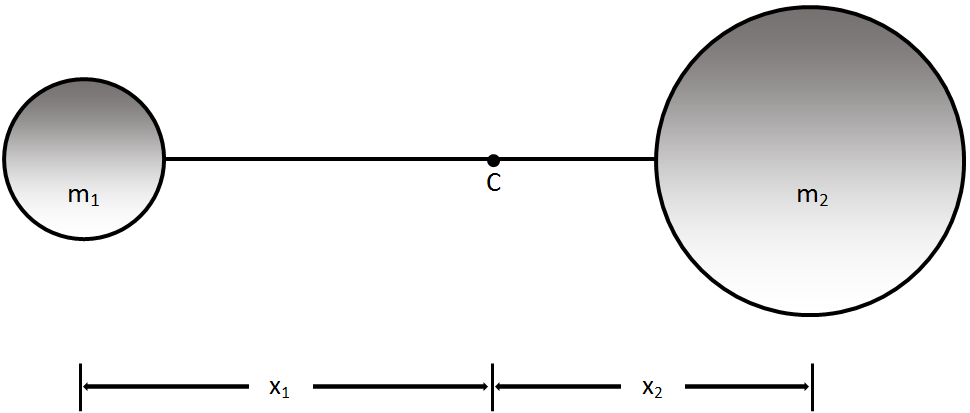
Let us suppose two bodies of masses m1 and m2 as shown in the figure. Let the masses be connected by a rigid rod and let C be their center of mass. Let x1 and x2 be the distance of m1 and m2 respectively from C. Then,