Bragg’s law was first proposed by Sir William Bragg and his son Sir Lawrence Bragg. They studied the diffraction of X-rays on various surfaces and defined the nature of x-rays diffraction on the crystal surface.
Basically, the law provides a relationship between the X-rays shooting on a crystal surface and its reflection from the surface.
Statement of Brag’s Law:
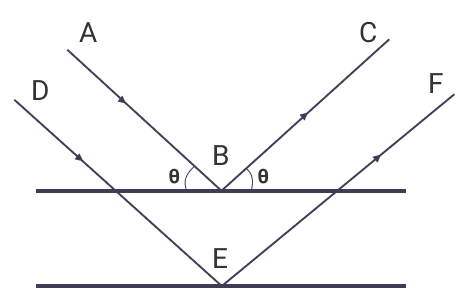
Suppose x-rays fall on a crystal plane with an incidence angle θ; then the rays are scattered from the crystal surfaces. During this process, some of the rays behave as if they were reflected from the surface, making the same angle θ. Hence, making the crystal plane behave like a mirror.
Bragg’s Equation
After observing the nature of x-rays diffraction, Bragg’s equation is created.
nλ = 2dSinθ
Here,
- d is the distance between two reflecting planes in a crystal
- θ is the incidence angle
- λ is the wavelength of x-rays
- n is an integer
Bragg’s equation gives us two important observation
- Angle of Incidence is equal to Angle of Reflection on a crystal plane.
- The path difference between two reflecting rays is equal to an integer number of the wavelength.
Derivation of Bragg’s Equation
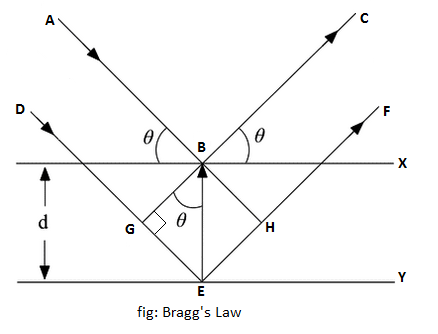
When monochromatic X-rays are incident upon a crystal, atoms in different layers act as a source of scattering radiation of the same wavelength, as shown in the above figure.
The intensity of the reflected beam will be maximum at a certain incident angle when the path difference between two reflected wave from two different planes is an integral multiple of the wavelength of X-rays.
That is, for maximum intensity,
path difference = nλ
where n is an integer: 1, 2, 3,... and λ is the wavelength.
From triangles BGE and BEH in the above figure,
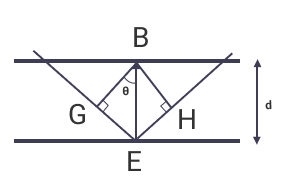
EH = GE = BEsinθ
or, EH = GE = dsinθ
GE is also the path difference between planes. Hence,
path difference = dsinθ
Combining two values of path difference, we get
nλ = dsinθ
This the Bragg’s equation of diffraction of x-rays.
Application of Bragg’s Law
1. Identify Crystal’s Atomic Structure
When x-rays fall on the crystal, atoms inside the crystal diffract the radiation. Now, by observing the pattern of diffracted rays, we can identify the structure of crystals.
2. Neutron and Electron Diffraction
We can apply the diffraction nature of Bragg’s law to both the neutron and electron diffraction processes.
Example: Find the spacing of atomic planes in the crystal using Bragg’s law
Suppose x-rays of wavelength 3.6 * 10-11 m undergo first-order reflection at an angle of 4.8° from the crystal. Find the spacing between atomic planes.
Given,
- Wavelength (λ) = 3.6 * 10-11 m
- Glancing angle(θ) = 4.8°
- Order of diffraction (n) = 1
Suppose the space between atomic planes be, d. According to Bragg’s equation,
nλ = dsinθ
or, 1 * 3.6 * 10-11 = d * sin4.8
or, d * 0.08367784 = 3.6 * 10-11
or, d = 3.6 * 10-11 / 0.08367784333
or, d = 4.3 * 10-10 m
Hence the spacing of the atomic planes is 4.3 * 10-10 m.
Related Articles